Process Synchronization

References:

1. Abraham Silberschatz, Greg Gagne, and Peter Baer Galvin, "Operating System Concepts, Ninth Edition ", Chapter 5

Warning: This chapter requires some heavy thought. As you read each of the algorithms below, you need to satisfy yourself that they do indeed work under all conditions. Think about it, and don't just accept them at face value.

5.1 Background

• Recall that back in Chapter 3 we looked at cooperating processes ( those that can effect or be effected by other simultaneously running processes ), and as an example, we used the producer-consumer cooperating processes:

  Producer code from chapter 3:

item nextProduced;

while( true ) {

/* Produce an item and store it in nextProduced */
nextProduced = makeNewItem( . . . );

/* Wait for space to become available */
while( ( ( in + 1 ) % BUFFER_SIZE ) == out )
      ; /* Do nothing */

/* And then store the item and repeat the loop. */
buffer[ in ] = nextProduced;
in = ( in + 1 ) % BUFFER_SIZE;

}

Consumer code from chapter 3:

item nextConsumed;

while( true ) {

/* Wait for an item to become available */
while( in == out )
      ; /* Do nothing */

/* Get the next available item */
nextConsumed = buffer[ out ];
out = ( out + 1 ) % BUFFER_SIZE;

/* Consume the item in nextConsumed
     ( Do something with it ) */

}

• The only problem with the above code is that the maximum number of items which can be placed into the buffer is BUFFER_SIZE - 1. One slot is unavailable because there always has to be a gap between the producer and the consumer.
• We could try to overcome this deficiency by introducing a counter variable, as shown in the following code segments:

• Unfortunately we have now introduced a new problem, because both the producer and the consumer are adjusting the value of the variable counter, which can lead to a condition known as a race condition. In this condition a piece of code may or may not work correctly, depending on which of two simultaneous processes executes first, and more importantly if one of the processes gets interrupted such that the other process runs between important steps of the first process. ( Bank balance example discussed in class. )
• The particular problem above comes from the producer executing "counter++" at the same time the consumer is executing "counter--". If one process gets part way through making the update and then the other process butts in, the value of counter can get left in an incorrect state.
• But, you might say, "Each of those are single instructions - How can they get interrupted halfway through?" The answer is that although they are single instructions in C++, they are actually three steps each at the hardware level: (1) Fetch counter from memory into a register, (2) increment or decrement the register, and (3) Store the new value of counter back to memory. If the instructions from the two processes get interleaved, there could be serious problems, such as illustrated by the following:

• Exercise: What would be the resulting value of counter if the order of statements T4 and T5 were reversed? ( What should the value of counter be after one producer and one consumer, assuming the original value was 5? )
• Note that race conditions are notoriously difficult to identify and debug, because by their very nature they only occur on rare occasions, and only when the timing is just exactly right. ( or wrong! :-) ) Race conditions are also very difficult to reproduce. :-(
• Obviously the solution is to only allow one process at a time to manipulate the value "counter". This is a very common occurrence among cooperating processes, so lets look at some ways in which this is done, as well as some classic problems in this area.

5.2 The Critical-Section Problem

• The producer-consumer problem described above is a specific example of a more general situation known as the critical section problem. The general idea is that in a number of cooperating processes, each has a critical section of code, with the following conditions and terminologies:
  • Only one process in the group can be allowed to execute in their critical section at any one time. If one process is already executing their critical section and another process wishes to do so, then the second process must be made to wait until the first process has completed their critical section work.
  • The code preceding the critical section, and which controls access to the critical section, is termed the entry section. It acts like a carefully controlled locking door.
  • The code following the critical section is termed the exit section. It generally releases the lock on someone else's door, or at least lets the world know that they are no longer in their critical section.
  • The rest of the code not included in either the critical section or the entry or exit sections is termed the remainder section.

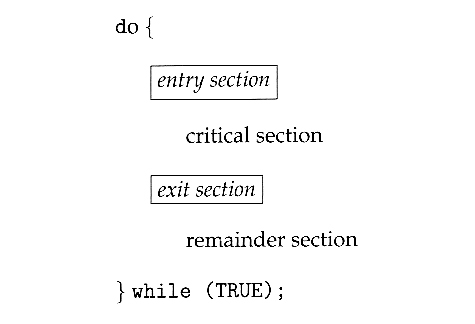
Figure 5.1 - General structure of a typical process Pi

• A solution to the critical section problem must satisfy the following three conditions:
  1. Mutual Exclusion - Only one process at a time can be executing in their critical section.
  2. Progress - If no process is currently executing in their critical section, and one or more processes want to execute their critical section, then only the processes not in their remainder sections can participate in the decision, and the decision cannot be postponed indefinitely. ( I.e. processes cannot be blocked forever waiting to get into their critical sections. )
  3. Bounded Waiting - There exists a limit as to how many other processes can get into their critical sections after a process requests entry into their critical section and before that request is granted. ( I.e. a process requesting entry into their critical section will get a turn eventually, and there is a limit as to how many other processes get to go first. )
• We assume that all processes proceed at a non-zero speed, but no assumptions can be made regarding the relative speed of one process versus another.
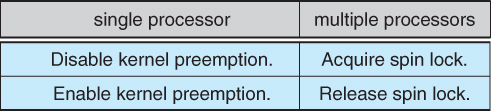
• Kernel processes can also be subject to race conditions, which can be especially problematic when updating commonly shared kernel data structures such as open file tables or virtual memory management. Accordingly kernels can take on one of two forms:
  • Non-preemptive kernels do not allow processes to be interrupted while in kernel mode. This eliminates the possibility of kernel-mode race conditions, but requires kernel mode operations to complete very quickly, and can be problematic for real-time systems, because timing cannot be guaranteed.
  • Preemptive kernels allow for real-time operations, but must be carefully written to avoid race conditions. This can be especially tricky on SMP systems, in which multiple kernel processes may be running simultaneously on different processors.
• Non-preemptive kernels include Windows XP, 2000, traditional UNIX, and Linux prior to 2.6; Preemptive kernels include Linux 2.6 and later, and some commercial UNIXes such as Solaris and IRIX.
  

5.3 Peterson's Solution

• Peterson's Solution is a classic software-based solution to the critical section problem. It is unfortunately not guaranteed to work on modern hardware, due to vagaries of load and store operations, but it illustrates a number of important concepts.
• Peterson's solution is based on two processes, P0 and P1, which alternate between their critical sections and remainder sections. For convenience of discussion, "this" process is Pi, and the "other" process is Pj. ( I.e. j = 1 - i )
• Peterson's solution requires two shared data items:
  • int turn - Indicates whose turn it is to enter into the critical section. If turn = = i, then process i is allowed into their critical section.
  • boolean flag[ 2 ] - Indicates when a process wants to enter into their critical section. When process i wants to enter their critical section, it sets flag[ i ] to true.
• In the following diagram, the entry and exit sections are enclosed in boxes.
  • In the entry section, process i first raises a flag indicating a desire to enter the critical section.
  • Then turn is set to j to allow the other process to enter their critical section if process j so desires.
  • The while loop is a busy loop ( notice the semicolon at the end ), which makes process i wait as long as process j has the turn and wants to enter the critical section.
  • Process i lowers the flag[ i ] in the exit section, allowing process j to continue if it has been waiting.

Figure 5.2 - The structure of process Pi in Peterson's solution.

• To prove that the solution is correct, we must examine the three conditions listed above:
  1. Mutual exclusion - If one process is executing their critical section when the other wishes to do so, the second process will become blocked by the flag of the first process. If both processes attempt to enter at the same time, the last process to execute "turn = j" will be blocked.
  2. Progress - Each process can only be blocked at the while if the other process wants to use the critical section ( flag[ j ] = = true ), AND it is the other process's turn to use the critical section ( turn = = j ). If both of those conditions are true, then the other process ( j ) will be allowed to enter the critical section, and upon exiting the critical section, will set flag[ j ] to false, releasing process i. The shared variable turn assures that only one process at a time can be blocked, and the flag variable allows one process to release the other when exiting their critical section.
  3. Bounded Waiting - As each process enters their entry section, they set the turn variable to be the other processes turn. Since no process ever sets it back to their own turn, this ensures that each process will have to let the other process go first at most one time before it becomes their turn again.
• Note that the instruction "turn = j" is atomic, that is it is a single machine instruction which cannot be interrupted.

5.4 Synchronization Hardware

• To generalize the solution(s) expressed above, each process when entering their critical section must set some sort of lock, to prevent other processes from entering their critical sections simultaneously, and must release the lock when exiting their critical section, to allow other processes to proceed. Obviously it must be possible to attain the lock only when no other process has already set a lock. Specific implementations of this general procedure can get quite complicated, and may include hardware solutions as outlined in this section.
• One simple solution to the critical section problem is to simply prevent a process from being interrupted while in their critical section, which is the approach taken by non preemptive kernels. Unfortunately this does not work well in multiprocessor environments, due to the difficulties in disabling and the re-enabling interrupts on all processors. There is also a question as to how this approach affects timing if the clock interrupt is disabled.
• Another approach is for hardware to provide certain atomic operations. These operations are guaranteed to operate as a single instruction, without interruption. One such operation is the "Test and Set", which simultaneously sets a boolean lock variable and returns its previous value, as shown in Figures 5.3 and 5.4:

Figures 5.3 and 5.4 illustrate "test_and_set( )" function

• Another variation on the test-and-set is an atomic swap of two booleans, as shown in Figures 5.5 and 5.6:

• The above examples satisfy the mutual exclusion requirement, but unfortunately do not guarantee bounded waiting. If there are multiple processes trying to get into their critical sections, there is no guarantee of what order they will enter, and any one process could have the bad luck to wait forever until they got their turn in the critical section. ( Since there is no guarantee as to the relative rates of the processes, a very fast process could theoretically release the lock, whip through their remainder section, and re-lock the lock before a slower process got a chance. As more and more processes are involved vying for the same resource, the odds of a slow process getting locked out completely increase. )
• Figure 5.7 illustrates a solution using test-and-set that does satisfy this requirement, using two shared data structures, boolean lock and boolean waiting[ N ], where N is the number of processes in contention for critical sections:

Figure 5.7 Bounded-waiting mutual exclusion with TestAndSet( ).

• The key feature of the above algorithm is that a process blocks on the AND of the critical section being locked and that this process is in the waiting state. When exiting a critical section, the exiting process does not just unlock the critical section and let the other processes have a free-for-all trying to get in. Rather it first looks in an orderly progression ( starting with the next process on the list ) for a process that has been waiting, and if it finds one, then it releases that particular process from its waiting state, without unlocking the critical section, thereby allowing a specific process into the critical section while continuing to block all the others. Only if there are no other processes currently waiting is the general lock removed, allowing the next process to come along access to the critical section.
• Unfortunately, hardware level locks are especially difficult to implement in multi-processor architectures. Discussion of such issues is left to books on advanced computer architecture.

5.5 Mutex Locks

• The hardware solutions presented above are often difficult for ordinary programmers to access, particularly on multi-processor machines, and particularly because they are often platform-dependent.
• Therefore most systems offer a software API equivalent called mutex locks or simply mutexes. ( For mutual exclusion )
• The terminology when using mutexes is to acquire a lock prior to entering a critical section, and to release it when exiting, as shown in Figure 5.8:

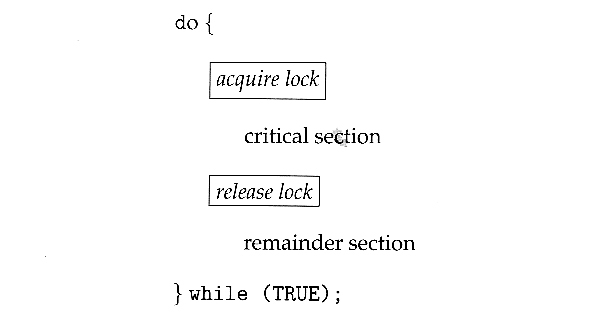
Figure 5.8 - Solution to the critical-section problem using mutex locks

• Just as with hardware locks, the acquire step will block the process if the lock is in use by another process, and both the acquire and release operations are atomic.
• Acquire and release can be implemented as shown here, based on a boolean variable "available":

• One problem with the implementation shown here, ( and in the hardware solutions presented earlier ), is the busy loop used to block processes in the acquire phase. These types of locks are referred to as spinlocks, because the CPU just sits and spins while blocking the process.
• Spinlocks are wasteful of cpu cycles, and are a really bad idea on single-cpu single-threaded machines, because the spinlock blocks the entire computer, and doesn't allow any other process to release the lock. ( Until the scheduler kicks the spinning process off of the cpu. )
• On the other hand, spinlocks do not incur the overhead of a context switch, so they are effectively used on multi-threaded machines when it is expected that the lock will be released after a short time.

5.6 Semaphores

• A more robust alternative to simple mutexes is to use semaphores, which are integer variables for which only two ( atomic ) operations are defined, the wait and signal operations, as shown in the following figure.
• Note that not only must the variable-changing steps ( S-- and S++ ) be indivisible, it is also necessary that for the wait operation when the test proves false that there be no interruptions before S gets decremented. It IS okay, however, for the busy loop to be interrupted when the test is true, which prevents the system from hanging forever.

5.6.1 Semaphore Usage

• In practice, semaphores can take on one of two forms:
  • Binary semaphores can take on one of two values, 0 or 1. They can be used to solve the critical section problem as described above, and can be used as mutexes on systems that do not provide a separate mutex mechanism.. The use of mutexes for this purpose is shown in Figure 6.9 ( from the 8th edition ) below.

  
  Mutual-exclusion implementation with semaphores. ( From 8th edition. )

  • Counting semaphores can take on any integer value, and are usually used to count the number remaining of some limited resource. The counter is initialized to the number of such resources available in the system, and whenever the counting semaphore is greater than zero, then a process can enter a critical section and use one of the resources. When the counter gets to zero ( or negative in some implementations ), then the process blocks until another process frees up a resource and increments the counting semaphore with a signal call. ( The binary semaphore can be seen as just a special case where the number of resources initially available is just one. )
  • Semaphores can also be used to synchronize certain operations between processes. For example, suppose it is important that process P1 execute statement S1 before process P2 executes statement S2.
    • First we create a semaphore named synch that is shared by the two processes, and initialize it to zero.
    • Then in process P1 we insert the code:

      S1;
      signal( synch );

    • and in process P2 we insert the code:

      wait( synch );
      S2;

    • Because synch was initialized to 0, process P2 will block on the wait until after P1 executes the call to signal.

5.6.2 Semaphore Implementation

• The big problem with semaphores as described above is the busy loop in the wait call, which consumes CPU cycles without doing any useful work. This type of lock is known as a spinlock, because the lock just sits there and spins while it waits. While this is generally a bad thing, it does have the advantage of not invoking context switches, and so it is sometimes used in multi-processing systems when the wait time is expected to be short - One thread spins on one processor while another completes their critical section on another processor.
• An alternative approach is to block a process when it is forced to wait for an available semaphore, and swap it out of the CPU. In this implementation each semaphore needs to maintain a list of processes that are blocked waiting for it, so that one of the processes can be woken up and swapped back in when the semaphore becomes available. ( Whether it gets swapped back into the CPU immediately or whether it needs to hang out in the ready queue for a while is a scheduling problem. )
• The new definition of a semaphore and the corresponding wait and signal operations are shown as follows:

• Note that in this implementation the value of the semaphore can actually become negative, in which case its magnitude is the number of processes waiting for that semaphore. This is a result of decrementing the counter before checking its value.
• Key to the success of semaphores is that the wait and signal operations be atomic, that is no other process can execute a wait or signal on the same semaphore at the same time. ( Other processes could be allowed to do other things, including working with other semaphores, they just can't have access to this semaphore. ) On single processors this can be implemented by disabling interrupts during the execution of wait and signal; Multiprocessor systems have to use more complex methods, including the use of spinlocking.

5.6.3 Deadlocks and Starvation

• One important problem that can arise when using semaphores to block processes waiting for a limited resource is the problem of deadlocks, which occur when multiple processes are blocked, each waiting for a resource that can only be freed by one of the other ( blocked ) processes, as illustrated in the following example. ( Deadlocks are covered more completely in chapter 7. )

• Another problem to consider is that of starvation, in which one or more processes gets blocked forever, and never get a chance to take their turn in the critical section. For example, in the semaphores above, we did not specify the algorithms for adding processes to the waiting queue in the semaphore in the wait( ) call, or selecting one to be removed from the queue in the signal( ) call. If the method chosen is a FIFO queue, then every process will eventually get their turn, but if a LIFO queue is implemented instead, then the first process to start waiting could starve.

5.6.4 Priority Inversion

• A challenging scheduling problem arises when a high-priority process gets blocked waiting for a resource that is currently held by a low-priority process.
• If the low-priority process gets pre-empted by one or more medium-priority processes, then the high-priority process is essentially made to wait for the medium priority processes to finish before the low-priority process can release the needed resource, causing a priority inversion. If there are enough medium-priority processes, then the high-priority process may be forced to wait for a very long time.
• One solution is a priority-inheritance protocol, in which a low-priority process holding a resource for which a high-priority process is waiting will temporarily inherit the high priority from the waiting process. This prevents the medium-priority processes from preempting the low-priority process until it releases the resource, blocking the priority inversion problem.
• The book has an interesting discussion of how a priority inversion almost doomed the Mars Pathfinder mission, and how the problem was solved when the priority inversion was stopped. Full details are available online at http://research.microsoft.com/en-us/um/people/mbj/mars_pathfinder/authoritative_account.htm

5.7 Classic Problems of Synchronization

The following classic problems are used to test virtually every new proposed synchronization algorithm.

5.7.1 The Bounded-Buffer Problem

• This is a generalization of the producer-consumer problem wherein access is controlled to a shared group of buffers of a limited size.
• In this solution, the two counting semaphores "full" and "empty" keep track of the current number of full and empty buffers respectively ( and initialized to 0 and N respectively. ) The binary semaphore mutex controls access to the critical section. The producer and consumer processes are nearly identical - One can think of the producer as producing full buffers, and the consumer producing empty buffers.

Figures 5.9 and 5.10 use variables next_produced and next_consumed

5.7.2 The Readers-Writers Problem

• In the readers-writers problem there are some processes ( termed readers ) who only read the shared data, and never change it, and there are other processes ( termed writers ) who may change the data in addition to or instead of reading it. There is no limit to how many readers can access the data simultaneously, but when a writer accesses the data, it needs exclusive access.
• There are several variations to the readers-writers problem, most centered around relative priorities of readers versus writers.
  • The first readers-writers problem gives priority to readers. In this problem, if a reader wants access to the data, and there is not already a writer accessing it, then access is granted to the reader. A solution to this problem can lead to starvation of the writers, as there could always be more readers coming along to access the data. ( A steady stream of readers will jump ahead of waiting writers as long as there is currently already another reader accessing the data, because the writer is forced to wait until the data is idle, which may never happen if there are enough readers. )
  • The second readers-writers problem gives priority to the writers. In this problem, when a writer wants access to the data it jumps to the head of the queue - All waiting readers are blocked, and the writer gets access to the data as soon as it becomes available. In this solution the readers may be starved by a steady stream of writers.
• The following code is an example of the first readers-writers problem, and involves an important counter and two binary semaphores:
  • readcount is used by the reader processes, to count the number of readers currently accessing the data.
  • mutex is a semaphore used only by the readers for controlled access to readcount.
  • rw_mutex is a semaphore used to block and release the writers. The first reader to access the data will set this lock and the last reader to exit will release it; The remaining readers do not touch rw_mutex. ( Eighth edition called this variable wrt. )
  • Note that the first reader to come along will block on rw_mutex if there is currently a writer accessing the data, and that all following readers will only block on mutex for their turn to increment readcount.

• Some hardware implementations provide specific reader-writer locks, which are accessed using an argument specifying whether access is requested for reading or writing. The use of reader-writer locks is beneficial for situation in which: (1) processes can be easily identified as either readers or writers, and (2) there are significantly more readers than writers, making the additional overhead of the reader-writer lock pay off in terms of increased concurrency of the readers.

5.7.3 The Dining-Philosophers Problem

• The dining philosophers problem is a classic synchronization problem involving the allocation of limited resources amongst a group of processes in a deadlock-free and starvation-free manner:
  • Consider five philosophers sitting around a table, in which there are five chopsticks evenly distributed and an endless bowl of rice in the center, as shown in the diagram below. ( There is exactly one chopstick between each pair of dining philosophers. )
  • These philosophers spend their lives alternating between two activities: eating and thinking.
  • When it is time for a philosopher to eat, it must first acquire two chopsticks - one from their left and one from their right.
  • When a philosopher thinks, it puts down both chopsticks in their original locations.

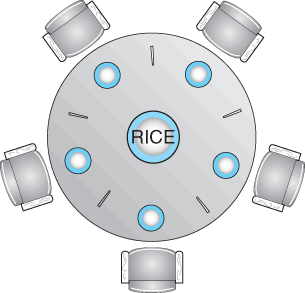
Figure 5.13 - The situation of the dining philosophers

• One possible solution, as shown in the following code section, is to use a set of five semaphores ( chopsticks[ 5 ] ), and to have each hungry philosopher first wait on their left chopstick ( chopsticks[ i ] ), and then wait on their right chopstick ( chopsticks[ ( i + 1 ) % 5 ] )
• But suppose that all five philosophers get hungry at the same time, and each starts by picking up their left chopstick. They then look for their right chopstick, but because it is unavailable, they wait for it, forever, and eventually all the philosophers starve due to the resulting deadlock.

Figure 5.14 - The structure of philosopher i.

• Some potential solutions to the problem include:
  • Only allow four philosophers to dine at the same time. ( Limited simultaneous processes. )
  • Allow philosophers to pick up chopsticks only when both are available, in a critical section. ( All or nothing allocation of critical resources. )
  • Use an asymmetric solution, in which odd philosophers pick up their left chopstick first and even philosophers pick up their right chopstick first. ( Will this solution always work? What if there are an even number of philosophers? )
• Note carefully that a deadlock-free solution to the dining philosophers problem does not necessarily guarantee a starvation-free one. ( While some or even most of the philosophers may be able to get on with their normal lives of eating and thinking, there may be one unlucky soul who never seems to be able to get both chopsticks at the same time. :-(

5.8 Monitors

• Semaphores can be very useful for solving concurrency problems, but only if programmers use them properly. If even one process fails to abide by the proper use of semaphores, either accidentally or deliberately, then the whole system breaks down. ( And since concurrency problems are by definition rare events, the problem code may easily go unnoticed and/or be heinous to debug. )
• For this reason a higher-level language construct has been developed, called monitors.

5.8.1 Monitor Usage

• A monitor is essentially a class, in which all data is private, and with the special restriction that only one method within any given monitor object may be active at the same time. An additional restriction is that monitor methods may only access the shared data within the monitor and any data passed to them as parameters. I.e. they cannot access any data external to the monitor.

Figure 5.15 - Syntax of a monitor.

• Figure 5.16 shows a schematic of a monitor, with an entry queue of processes waiting their turn to execute monitor operations ( methods. )

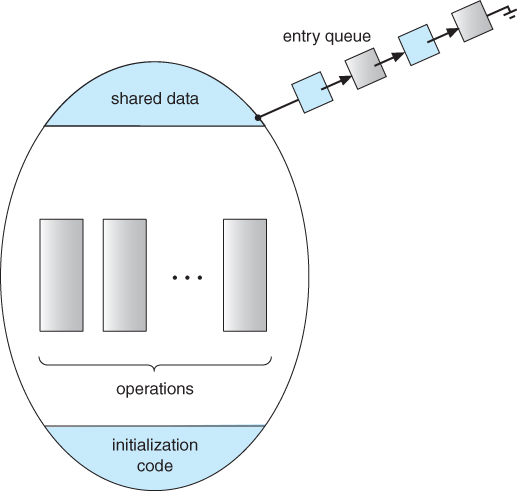
Figure 5.16 - Schematic view of a monitor

• In order to fully realize the potential of monitors, we need to introduce one additional new data type, known as a condition.
  • A variable of type condition has only two legal operations, wait and signal. I.e. if X was defined as type condition, then legal operations would be X.wait( ) and X.signal( )
  • The wait operation blocks a process until some other process calls signal, and adds the blocked process onto a list associated with that condition.
  • The signal process does nothing if there are no processes waiting on that condition. Otherwise it wakes up exactly one process from the condition's list of waiting processes. ( Contrast this with counting semaphores, which always affect the semaphore on a signal call. )
• Figure 6.18 below illustrates a monitor that includes condition variables within its data space. Note that the condition variables, along with the list of processes currently waiting for the conditions, are in the data space of the monitor - The processes on these lists are not "in" the monitor, in the sense that they are not executing any code in the monitor.

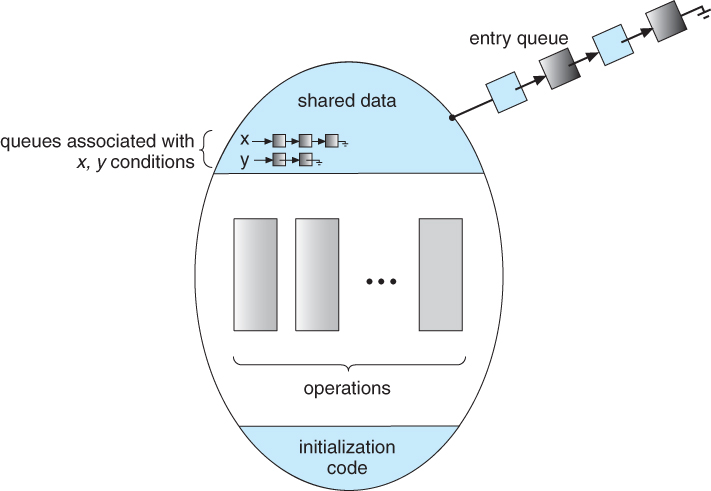
Figure 5.17 - Monitor with condition variables

• But now there is a potential problem - If process P within the monitor issues a signal that would wake up process Q also within the monitor, then there would be two processes running simultaneously within the monitor, violating the exclusion requirement. Accordingly there are two possible solutions to this dilemma:

Signal and wait - When process P issues the signal to wake up process Q, P then waits, either for Q to leave the monitor or on some other condition.

Signal and continue - When P issues the signal, Q waits, either for P to exit the monitor or for some other condition.

There are arguments for and against either choice. Concurrent Pascal offers a third alternative - The signal call causes the signaling process to immediately exit the monitor, so that the waiting process can then wake up and proceed.

• Java and C# ( C sharp ) offer monitors bulit-in to the language. Erlang offers similar but different constructs.

5.8.2 Dining-Philosophers Solution Using Monitors

• This solution to the dining philosophers uses monitors, and the restriction that a philosopher may only pick up chopsticks when both are available. There are also two key data structures in use in this solution:
  1. enum { THINKING, HUNGRY,EATING } state[ 5 ]; A philosopher may only set their state to eating when neither of their adjacent neighbors is eating. ( state[ ( i + 1 ) % 5 ] != EATING && state[ ( i + 4 ) % 5 ] != EATING ).
  2. condition self[ 5 ]; This condition is used to delay a hungry philosopher who is unable to acquire chopsticks.
• In the following solution philosophers share a monitor, DiningPhilosophers, and eat using the following sequence of operations:
  1. DiningPhilosophers.pickup( ) - Acquires chopsticks, which may block the process.
  2. eat
  3. DiningPhilosophers.putdown( ) - Releases the chopsticks.

5.8.3 Implementing a Monitor Using Semaphores

• One possible implementation of a monitor uses a semaphore "mutex" to control mutual exclusionary access to the monitor, and a counting semaphore "next" on which processes can suspend themselves after they are already "inside" the monitor ( in conjunction with condition variables, see below. ) The integer next_count keeps track of how many processes are waiting in the next queue. Externally accessible monitor processes are then implemented as:

• Condition variables can be implemented using semaphores as well. For a condition x, a semaphore "x_sem" and an integer "x_count" are introduced, both initialized to zero. The wait and signal methods are then implemented as follows. ( This approach to the condition implements the signal-and-wait option described above for ensuring that only one process at a time is active inside the monitor. )

5.8.4 Resuming Processes Within a Monitor

• When there are multiple processes waiting on the same condition within a monitor, how does one decide which one to wake up in response to a signal on that condition? One obvious approach is FCFS, and this may be suitable in many cases.
• Another alternative is to assign ( integer ) priorities, and to wake up the process with the smallest ( best ) priority.
• Figure 5.19 illustrates the use of such a condition within a monitor used for resource allocation. Processes wishing to access this resource must specify the time they expect to use it using the acquire( time ) method, and must call the release( ) method when they are done with the resource.

Figure 5.19 - A monitor to allocate a single resource.

• Unfortunately the use of monitors to restrict access to resources still only works if programmers make the requisite acquire and release calls properly. One option would be to place the resource allocation code into the monitor, thereby eliminating the option for programmers to bypass or ignore the monitor, but then that would substitute the monitor's scheduling algorithms for whatever other scheduling algorithms may have been chosen for that particular resource. Chapter 14 on Protection presents more advanced methods for enforcing "nice" cooperation among processes contending for shared resources.
• Concurrent Pascal, Mesa, C#, and Java all implement monitors as described here. Erlang provides concurrency support using a similar mechanism.

5.9 Synchronization Examples ( Optional )

This section looks at how synchronization is handled in a number of different systems.

5.9.1 Synchronization in Windows

Figure 5.20 - Mutex dispatcher object

5.9.2 Synchronization in Linux

5.9.3 Synchronization in Solaris

• Solaris controls access to critical sections using five tools: semaphores, condition variables, adaptive mutexes, reader-writer locks, and turnstiles. The first two are as described above, and the other three are described here:

Adaptive Mutexes

• Adaptive mutexes are basically binary semaphores that are implemented differently depending upon the conditions:
  • On a single processor system, the semaphore sleeps when it is blocked, until the block is released.
  • On a multi-processor system, if the thread that is blocking the semaphore is running on the same processor as the thread that is blocked, or if the blocking thread is not running at all, then the blocked thread sleeps just like a single processor system.
  • However if the blocking thread is currently running on a different processor than the blocked thread, then the blocked thread does a spinlock, under the assumption that the block will soon be released.
  • Adaptive mutexes are only used for protecting short critical sections, where the benefit of not doing context switching is worth a short bit of spinlocking. Otherwise traditional semaphores and condition variables are used.

Reader-Writer Locks

• Reader-writer locks are used only for protecting longer sections of code which are accessed frequently but which are changed infrequently.

Turnstiles

• A turnstile is a queue of threads waiting on a lock.
• Each synchronized object which has threads blocked waiting for access to it needs a separate turnstile. For efficiency, however, the turnstile is associated with the thread currently holding the object, rather than the object itself.
• In order to prevent priority inversion, the thread holding a lock for an object will temporarily acquire the highest priority of any process in the turnstile waiting for the blocked object. This is called a priority-inheritance protocol.
• User threads are controlled the same as for kernel threads, except that the priority-inheritance protocol does not apply.

5.9 4 Pthreads Synchronization( was 6.8.4 )

5.10 Alternate Approaches ( Optional )

5.10.1 Transactional Memory

5.10.2 OpenMP

5.10.3 Functional Programming Languages

5.11 Summary

Old 6.9 Atomic Transactions ( Optional, Not in Ninth Edition )

• Database operations frequently need to carry out atomic transactions, in which the entire transaction must either complete or not occur at all. The classic example is a transfer of funds, which involves withdrawing funds from one account and depositing them into another - Either both halves of the transaction must complete, or neither must complete.
• Operating Systems can be viewed as having many of the same needs and problems as databases, in that an OS can be said to manage a small database of process-related information. As such, OSes can benefit from emulating some of the techniques originally developed for databases. Here we first look at some of those techniques, and then how they can be used to benefit OS development.

6.9.1 System Model

• A transaction is a series of actions that must either complete in its entirety or must be rolled-back as if it had never commenced.
• The system is considered to have three types of storage:
  • Volatile storage usually gets lost in a system crash.
  • Non-volatile storage usually survives system crashes, but may still get lost.
  • Stable storage "never" gets lost or damaged. In practice this is implemented using multiple copies stored on different media with different failure modes.

6.9.2 Log-Based Recovery

• Before each step of a transaction is conducted, a entry is written to a log on stable storage:
  • Each transaction has a unique serial number.
  • The first entry is a "start"
  • Every data changing entry specifies the transaction number, the old value, and the new value.
  • The final entry is a "commit".
  • All transactions are idempotent - The can be repeated any number of times and the effect is the same as doing them once. Likewise they can be undone any number of times and the effect is the same as undoing them once. ( I.e. "change x from 5 to 6", rather than "add 1 to x" ).
• After a crash, any transaction which has "commit" recorded in the log can be redone from the log information. Any which has "start" but not "commit" can be undone.

6.9.3 Checkpoints

• In the event of a crash, all data can be recovered using the system described above, by going through the entire log and performing either redo or undo operations on all the transactions listed there.
• Unfortunately this approach can be slow and wasteful, because many transactions are repeated that were not lost in the crash.
• Alternatively, one can periodically establish a checkpoint, as follows:
  • Write all data that has been affected by recent transactions ( since the last checkpoint ) to stable storage.
  • Write a <checkpoint> entry to the log.
• Now for crash recovery one only needs to find transactions that did not commit prior to the most recent checkpoint. Specifically one looks backwards from the end of the log for the last <checkpoint> record, and then looks backward from there for the most recent transaction that started before the checkpoint. Only that transaction and the ones more recent need to be redone or undone.

6.9.4 Concurrent Atomic Transactions

• All of the previous discussion on log-based recovery assumed that only one transaction could be conducted at a time. We now relax that restriction, and allow multiple transactions to occur concurrently, while still keeping each individual transaction atomic.

6.9.4.1 Serializability

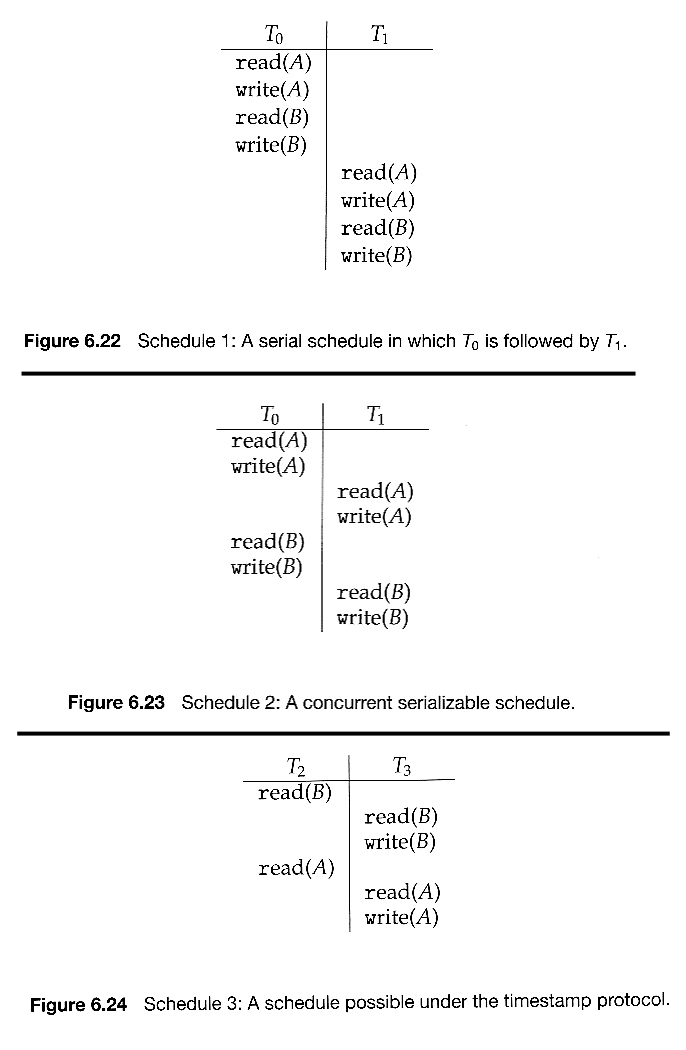
• Figure 6.22 below shows a schedule in which transaction 0 reads and writes data items A and B, followed by transaction 1 which also reads and writes A and B.
• This is termed a serial schedule, because the two transactions are conducted serially. For any N transactions, there are N! possible serial schedules.
• A nonserial schedule is one in which the steps of the transactions are not completely serial, i.e. they interleave in some manner.
• Nonserial schedules are not necessarily bad or wrong, so long as they can be shown to be equivalent to some serial schedule. A nonserial schedule that can be converted to a serial one is said to be conflict serializable, such as that shown in Figure 6.23 below. Legal steps in the conversion are as follows:
  • Two operations from different transactions are said to be conflicting if they involve the same data item and at least one of the operations is a write operations. Operations from two transactions are non-conflicting if they either involve different data items or do not involve any write operations.
  • Two operations in a schedule can be swapped if they are from two different transactions and if they are non-conflicting.
  • A schedules is conflict serializable if there exists a series of valid swap that converts the schedule into a serial schedule.

6.9.4.2 Locking Protocol

• One way to ensure serializability is to use locks on data items during atomic transactions.
• Shared and Exclusive locks correspond to the Readers and Writers problem discussed above.
• The two-phase locking protocol operates in two phases:
  • A growing phase, in which the transaction continues to gain additional locks on data items as it needs them, and has not yet relinquished any of its locks.
  • A shrinking phase, in which it relinquishes locks. Once a transaction releases any lock, then it is in the shrinking phase and cannot acquire any more locks.
• The two-phase locking protocol can be proven to yield serializable schedules, but it does not guarantee avoidance of deadlock. There may also be perfectly valid serializable schedules that are unobtainable with this protocol.

6.9.4.3 Timestamp-Based Protocols

• Under the timestamp protocol, each transaction is issued a unique timestamp entry before it begins execution. This can be the system time on systems where all process access the same clock, or some non-decreasing serial number. The timestamp for transaction Ti is denoted TS( Ti )
• The schedules generated are all equivalent to a serial schedule occurring in timestamp order.
• Each data item also has two timestamp values associated with it - The W-timestamp is the timestamp of the last transaction to successfully write the data item, and the R-timestamp is the stamp of the last transaction to successfully read from it. ( Note that these are the timestamps of the respective transactions, not the time at which the read or write occurred. )
• The timestamps are used in the following manner:
  • Suppose transaction Ti issues a read on data item Q:
    • If TS( Ti ) < the W-timestamp for Q, then it is attempting to read data that has been changed. Transaction Ti is rolled back, and restarted with a new timestamp.
    • If TS( Ti ) > the W-timestamp for Q, then the R-timestamp for Q is updated to the later of its current value and TS( Ti ).
  • Suppose Ti issues a write on Q:
    • If TS( Ti ) < the R-timestamp for Q, then it is attempting to change data that has already been read in its unaltered state. Ti is rolled back and restarted with a new timestamp.
    • If TS( Ti ) < the W-timestamp for Q it is also rolled back and restarted, for similar reasons.
    • Otherwise, the operation proceeds, and the W-timestamp for Q is updated to TS( Ti ).