
Electronic Proceedings
of the
ACM Workshop on Effective Abstractions in Multimedia
November 4, 1995
San Francisco, California
The recent advances in multimedia systems, together with the advent of high speed networks, paved the way to a new generation of applications. In particular, the authoring environments found in multimedia the means of increasing the richness of the information contained in electronic documents. With the evolution of new computer systems handling multimedia information, time-based data can be integrated in electronic documents taking into account their temporal dimension. In such documents, temporal dependencies between the different media objects define a temporal structure within the document. This structure is the basic support for the representation of dependencies between data like audio, video and virtual images. Furthermore, it allows the scheduling of presentation actions during the document presentation.
In traditional documents, objects do not have a notion of time. This means that the author does not have to specify neither the overall duration of the presentation, nor when and for how long single media objects are presented. In contrast, the presentation of multimedia documents is dynamic and the positioning of objects in time together with their duration have to be specified. To achieve efficiently this operation, high level temporal representations are needed. These representations serve to capture, at the author's level, all the temporal dependencies between multimedia objects.
In this paper, we address the problems related to the temporal consistency of multimedia documents. We propose a complete set of operators to represent the temporal structure of multimedia documents and an efficient algorithm allowing the detection of a wide range of inconsistencies. The emphasis in the design of these algorithms is put on the handling of both the flexibility of temporal specifications and the unpredictable behaviour of intervals. Furthermore, we use the logical organization of the document in nested entities to enhance the performance of the methods used for detecting inconsistencies. The aim of our approach is to address the following requirements :
A temporal model is a set of abstractions that allow users to specify temporal constraints in multimedia documents. This model consists of a given representation of time (a time model), a temporal expression that defines a temporal language and some capabilities or mechanisms for automatically processing the temporal information contained in multimedia documents.
The basic parameter of a temporal relation is an interval, which is an abstraction of a media object. This interval has a non-zero duration and is described in the time space by two instants or end points (begin, end). This duration can be an intrinsic information of the media object or dependent on some constraints in the context of a given document. In our model, we distinguish between three kinds or classes of basic media objects regarding their temporal behaviour[LAY 95] :
A multimedia document, tough its apparent compactness, is a mixture of sub-components which are related by several types of relationships. These various natures of bindings confer to the document a multi-dimensional skeleton which reflects its spatial, temporal, logical and semantical (hypermedia) structure.
In the context of a given document, objects are logically organized as a collection of nested entities (document scenes). This organization of the document is achieved to construct pieces of information so that semantically related elements build a new atomic entity with higher granularity. We call this operation the logical composition of the document and, as defined here, this dimension of the document deals only with the manner of how the encapsulation of multimedia components is performed. Usually, existing models do not make a clear difference between the logical and the temporal dimensions since they use the temporal operators to build logical clusters.
In our approach, a multimedia document is considered as an organized set of typed elements which are logically related to each other. Typical elements of these documents are titles, paragraphs, tables, graphics, figures, 3D animation, audio, video, etc. All these elements have various structural relationships: a movie contains a video, some paragraphs and optionally a background music; a scene follows another scene; a part of an image may refer to a section item, etc. International standards like SGML[GOL 90] or HyTime[HYT 92] have extended this approach by defining classes of documents or DTDs (Document Type Definitions). A DTD is a BNF-like grammar that describes the document content and drives the authoring process through the user interface[QUI 86] [LAY 95] . Several works have used the structuring scheme to automatically produce spatial layout in classical documents[ROI 94] [LAM 86] . We claim that similar work can be achieved for the temporal dimension.
Temporal composition is a language driven process that defines the temporal synchronization of multimedia objects. Generally, temporal languages are based on a functional description so that encapsulation becomes straightforward [HAR 93] [LIT 93] . The drawbacks of these formalisms is that encapsulation is achieved at the cost of the temporal language expressiveness, since the temporal representation of the document is restricted to a tree structure[LIT 93] . In contrast, some other models uses a relational way of composition which permits a maximal temporal expressiveness[BUC 93] . However, they do not take advantage of the encapsulation suitable for a modular composition, a better reuse and a higher efficiency in maintaining the overall temporal consistency of the document.
Our model is based on the general relational model of Allen [ALL 83] extended to take into account both the quantitative aspect of intervals and delays and the nesting of logical parts of multimedia documents. We believe that this method provides a better compromise between the expressiveness of the temporal language and the efficiency of the consistency checking algorithms.
First, we must distinguish between symbolic specifications and numerical constraints. Symbolic specifications are primitive relations introduced by Allen and possibly their disjunctions permitted by the pointizable interval algebra [VIL 86] . This restricted algebra can be translated into time point algebra relations and the associated numerical constraint propagation methods can be achieved in a polynomial time. In our temporal language, we restrict the set of operators to the non-disjunctive case called STP (Simple Temporal Problems [VIL 86] [GHA 93] ). This symbolic representation allows the user to set the temporal constraints of the document through a high level interface.

Figure 1 - The set of temporal operators
From the point of view of the author, the temporal structure of a multimedia document is defined as a graph G with at least one vertex and a set of edges where each edge v -- Rx (t) --> w connects a pair of vertices v and w with is one of the relations described in Fig. 1 , v and w are object names and t is the delay attached to the relation if any. This graph is called the symbolic temporal graph since temporal constraints, multimedia objects and delays are represented by their symbols or names (see example in Fig. 2 ).
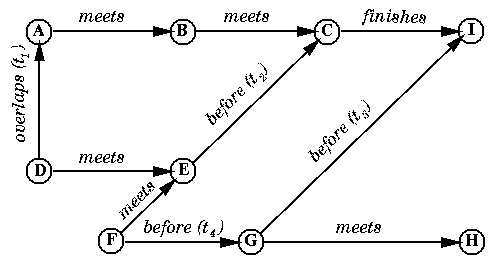
Figure 2 - Abstract Temporal Structure
Each vertex of the symbolic graph G represents a multimedia object MO. A multimedia object could be:
The notion of container matches, in fact, the paradigm of logical composition of multimedia objects introduced earlier. Furthermore, there is a more general definition of a container which takes into account its various dimensions. It defines a container as an isolated part of the document which is spatially, temporally and logically independent. Therefore, it is synchronized with the other objects only through its end points. When some components of a document are grouped as a container, all their mutual synchronization constraints, and consequently, their final presentation are fully specified. This property ensures the global consistency of the multimedia document during the authoring stage.
A basic media object BMO is described by a set of attributes. These attributes reflect the temporal nature of the object and are as follows :
Attributes of BMO = { Name, Type, Duration }
The attribute Name is a global identifier that allows the access to object at the storage. The attribute Type defines the temporal type of the object and takes the values { Discrete, Continuous, Indeterministic }. The Duration attribute is the allowable range of durations that can be applied to the object at the presentation stage. This last attribute can also have the value Indefinite for those objects whose type is Indeterministic. Containers have a similar set of attributes but their values are deduced from the attributes of the objects they encapsulate (see Section 3).
In practice, documents are produced following an edit and pre-view cycle. This process is inherently incremental and allows a progressive tuning of the final presentation. When editing a document, authors add information by introducing new media objects, or by specifying new temporal constraints in the symbolic graph.
But modifying a document requires that the editor supports some functionalities to insure that for every specification introduced by the author, the overall document remains consistent (its presentation is possible given the set of constraints specified by the author).
Modifying a document by incremental specification of new objects and relations, introduce additional temporal constraints. This operation may lead to a temporal inconsistency because temporal parameters of objects (duration, begin-end dates) must satisfy invariants related to the time progression and causality. For example (see Fig. 3 -a), given three objects a, b and c, specifying that a meets b and b meets c make inconsistent the further specification c overlaps a. This is called a qualitative inconsistency because it results from the nature of the relations independently of the durations of objects they link. However, qualitative consistent specifications may be inconsistent regarding the explicit durations of the related objects. For example (see Fig. 3 -b), specifying that a meets b and a starts c make inconsistent the further qualitative consistent specification c overlaps b if duration (a)=3 seconds and duration (c)=2 seconds. Finally, in the example Fig. 3 -c, we expose another type of inconsistencies due to the presence of indeterministic intervals. Given three objects a, b and c where duration (a)=3 seconds, duration (b)=2 seconds and c is an indeterministic object whose duration is bounded in the interval [2, 4], specifying that a meets b, a starts c and c overlaps b leads to an inconsistency since the end of c may occur at any time, therefore this specification may possibly fail.
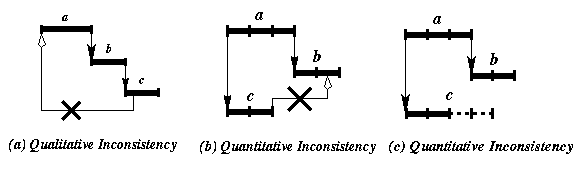
Figure 3 - Temporal inconsistency examples
Most of the authoring systems which provide interval based paradigms of multimedia documents specification propose incomplete algorithms of consistency checking or prefer to reduce the set of temporal relations to avoid inconsistencies. In all cases, they don't take into account the quantitative consistency detection nor the indeterministic behaviour of some intervals. We expose in the following section a way to address both the problem of maintaining the temporal consistency in presence of indeterministic media objects and the efficiency of the algorithm achieving this operation.
In the classification of multimedia objects introduced in Section 2 , we distinguish between discrete, continuous and indeterministic objects. At the abstract level, all these types of objects as well as the delays can be represented as intervals with given durations. But when considering the mechanism of constraints propagation, one can notice a fundamental difference between two types of intervals: free or contingent.
Definition1 : A free interval is an interval with a numerical constraint [l, u]f (where l<u, l and u are positive values and where u can have an infinite value) on the duration such that its value can be freely assigned in the domain [l, u]. This kind of intervals models the behaviour of continuous objects whose durations can be chosen in a finite range according to allowable play-back rates or discrete objects whose durations can be assigned any value ( the range, in this particular case, is infinite).
Definition2 : A contingent interval is an interval with a numerical constraint [l, u]c on its duration which is a random value in the domain [l, u]. This kind of intervals models the behaviour of indeterministic objects whose values are random.
Following these two definitions, we can distinguish between two aspects of a temporal scenario : the flexibility and the controllability. The flexibility measures the ability of a temporal scenario to be adjusted in order to meet the consistency requirements. It can be achieved using the free delays and the properties of some multimedia objects to be shrinked or stretched in a given domain of durations. This domain is generally chosen in such a way that preserves the intelligibility of these objects at the presentation time. As we will see in the next section, flexibility will also be used to tackle the indeterministic behaviour of contingent intervals and consequently the consistency checking methods. The controllability of a temporal scenario means the possibility to re-adjust it in order to compensate, at run-time, the behaviour of indeterministic objects.
From the abstract representation of a document presented in section 2 , we extract a lower level representation of the temporal structure to model the underlying numerical constraints. This representation defines a multimedia document as a Directed Acyclic Graph (DAG) where nodes are the begin-end dates of multimedia objects and the edges are numerical constraints on the durations as defined in Fig. 1 . These numerical constraints reflects the allowable durations of intervals and delays specified as the parameters of temporal relations. We add two abstract time-points Begin and End corresponding to the dates of the beginning and the end of a given container. The Begin time point is related by edges labeled with particular delays to all time-points which do not have incoming edges. Similarly, all the time points with no outgoing edges are related to the End time point. This representation of the document is the basic data structure that we use to hold the numerical constraints of the entire document. Fig. 4 shows an example of a DAG corresponding to our previous example of Fig. 2 .
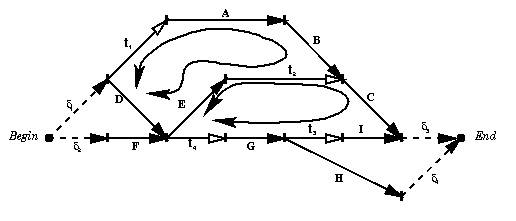
Figure 4 - Temporal Directed Acyclic Graph
First, let us introduce the notion of temporal chains. A temporal chain [ e1, e2, .., en] is a sequence of contiguous edges where each edge ej , 1 < j < n is only related to one successor and one predecessor so that begin ( ej ) = end ( ej-1) and end ( ej ) = begin ( ej+1), every single interval being free or contingent.
Given the DAG representation extracted from the temporal operators graph, we can make the following statements :
These two statements distinguish the sources of the three types of inconsistencies introduced earlier. First, we make a fundamental assumption about the observance of the scenario at run-time. Since the specification stage of a temporal scenario is somehow a prediction of how events will occur over time, we assume that the only observable states of the temporal scenario at run-time are the end-points of the intervals.The main idea behind this assumption is to provide by static methods the means for deciding if a given scenario can be dynamically adjusted or not. Our algorithm uses these observable states of the presentation in two stages: first, to establish the effective durations of unpredictable intervals, then to compensate these random delays by a provision of flexibility taken from forthcoming intervals called provision intervals. The amount of flexibility provisions corresponds to the worst case execution so we can guarantee in all the cases the consistency of the presentation. The provisions of flexibility are simply reserved by reducing the range of flexible intervals by the same amount. Note that the value of random delays must be observed before the provision interval has started during the presentation because of our assumption, except for discrete objects whose end can be delayed arbitrarily. Before getting in the description of the algorithm, let us first expose how this way of checking the temporal compatibility of two chains works through simple examples.
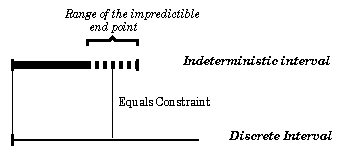
Figure 5 - Example of scenario adjustment using a discrete interval
In this first example (see Fig. 5 ), the user has specified an equality between an indeterministic object A and a discrete object B. The first object is represented in the DAG by a contingent interval whose duration is in the range [l,u]c. It is straightforward that this scenario is consistent since the end of the object B (represented by a free interval [0, infinite]f) can be freely delayed until the occurrence of the end instant of object A, whenever this happens.
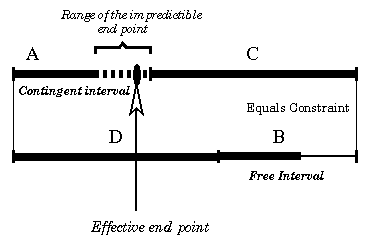
Figure 6 - Example of scenario adjustment by reducing the flexibility of a free interval
In this second example, we take a part of a scenario where we have two chains that are constrained to be of equal durations. In order to satisfy this constraint we have to ensure that begin and end points of these chains start and finish at the same time. The object A is an indeterministic object whose end point can occur at any time in the range represented by a dashed line (see Fig. 6 ). The object B is a continuous object with an amount of flexibility represented by a thin line in the figure. Here again, it is easy to see that if the amount of flexibility of the object B is higher than the unpredictable range of the object A (condition1), and if the the observable point precedes the start point of the object B (condition 2), then the temporal coincidence of the end instant of the objects C and B can be achieved. Therefore this part of the scenario is consistent since it is controllable.
One can notice that a given chain, if considered through its end points, defines a new interval, and therefore its total duration can be reduced into two parts, one part representing the total duration of free intervals and another part for contingent ones as follows :
Let C be a chain containing the sequence A1, A2, ..., An of intervals, each interval A has a duration [L, U] and can be free or contingent. Note that a given chain can be considered as a free interval if it contains only free intervals, and contingent if it contains at least one contingent interval. The total duration of a chain and some of its parameters are defined as follows (sum is the n-ary addition operator):
Duration_Range (C) = Free_Range(C) union Contingent_Range(C)
Free_Range(C) = [sum(Li),sum(Ui)]f = [CLF, CUF]f
Contingent_Range(C) = [sum(Lj),sum(Uj)]c = [CLC, CUC]c
Flexibility_Amount(C) = CUF - CLF
Indeterministic_Amount(C) = CUC - CLC
Where Ui is the set of free intervals of the chain and Uj of contingent ones.
The consistency checking algorithm which is based on the previous assumption and statements works according to these four stages :
For each new specification
Stage 1 (qualitative consistency)
If the new relation introduces a circuit in the DAG then this specification leads to a qualitative inconsistency (statement 1). It is therefore rejected.
Stage 2 (forming the chains)
If it introduces new cycles, we build the corresponding temporal chains that we add to the existing ones representing the other cycles (if any). Each duration range of these chains is then computed as described earlier. As a result, the numerical constraints of the whole document are, after this stage, represented by this set of chains through their free and contingent duration ranges. The temporal consistency of the scenario is then reduced to the problem of finding a combination of values that ensures, for every cycle of the graph, the temporal coincidence of its two end points. Since we proceed by incremental steps, this operation is first achieved for the new chains then for the other depending chains (progressive propagation of the constraints).
Stage 3 (testing the quantitative consistency)
The newly introduced chains are then checked one by one against the existing ones as follows: As we have four possible combinations of chains depending on their behaviour (free/contingent), a first pass of the algorithm is used to solve some trivial cases by checking some necessary conditions on the durations ranges.
For every cycle composed of two chains C1 and C2 :
if (C1 is free) and (C2 is free) then
Range == Duration_Range(C1) intersection Duration_range(C2)
if range == Null then Inconsistent, goto stage 4
else
Ind = Indeterministic_Amount(C1) + Indeterministic_Amount(C2)
if range == Null then Inconsistent, goto stage 4
else
Ind = Indeterministic_Amount(C1) + Indeterministic_Amount(C2)
Free = Flexibility_Amount(C1)+Flexibility_Amount(C2)
if (Ind > Free) then Inconsistent, goto stage 4
else /* all the other cases */
if Adapt (C1, C2) == True Then /*success , proceed with the next cycle */
else Inconsistent, goto stage 4
End
The function Adapt (C1, C2) looks for a correspondence between contingent intervals contained in C1 and C2 and forthcoming flexible intervals in a way that recovers all the indeterministic behaviour. Here again some trivial cases arises, for exemple two chains can not be ended by contingent intervals since one can not guarantee that their two end-points finishes at the same time. In the general case, for each contingent interval c, the choise of corresponding recovery interval is based on the following hint : if c belongs to C1 and the duration of C1 is less than the duration of C2, we try first to find a recovery interval in C1 so that the overall durations of C1 and C2 gets closer, otherwise we look for one in C2. At the end of this stage, if all the contingent intervals have been recovered and the durations of C1 and C2 are still intersecting, then we have found a solution, in all the other cases our method fails (jump to stage 4).
Stage 4 (Restoring the previous state of the document)
In this stage, an inconsistency was found, therefore we restore the state of the document as it was before the step 1, and an error is then reported to the author.
This algorithm is applied to check the consistency of both the entire document and single containers defined by the user. Containers are considered at each level of the logical structure as a single interval with its own total duration (with a free and contingent part). This total duration corresponds to maximum duration of the Begin-End paths in the DAG.
Our current algorithm is a first step in extending the temporal synchronization methods to handle indeterministic behaviour of multimedia objects. We have shown that this kind of objects can be included in the model by separating free intervals from contingent ones. This latter class of intervals models a wide range of multimedia objects like impredictible delays in media delivery and user interactions. As we have shown through simple examples one can handle such situations using similar techniques. Our algorithm based on the Adapt function is not minimal. Since we use an opportunistic method to choose recovery intervals, some of the configurations are not solved even if a solution exists. We are currently investigating recent methods developped in planning systems which provides minimal solutions [FAR 95] [DUB 93] .
We presented in this paper a temporal model that allows the construction of consistent temporal presentations. The consistency is performed using qualitative as well as quantitative temporal relations through constraint networks. The user interface is based on the set of operators introduced by Allen, extended to the quantitative aspect of intervals, delays and unpredictible behaviour. In particular, our model allows the representation of indeterministic objects which have unpredictable durations. In the design of this algorithm, we put the emphasis on the following aspects :
This work is currently experimented in the Opera project. The goal of this project is to develop an editorial environment for the construction, manipulation and storage of complex multimedia documents. The Opera system is based on a logical document structuring scheme that was introduced and tested during the development of the Grif editor [QUI 86] .